I began my forty-year career in education as a middle school math teacher. When I briefly took time to stay home and raise my children, I co-authored two math workbooks for McGraw Hill and taught developmental math and math education courses to undergraduate and graduate students at Rutgers University. I also worked with researchers at Rutgers and helped begin a long-term K-8 teacher development project, leading workshops in mathematics and providing model lessons in classrooms.
I returned to work as an assistant principal in a K-4 school. Part of my job was teaching enrichment math classes to 3rd and 4th graders and providing math staff development to K-6 teachers. I moved from there to become principal in a K-4 school. For the next ten years I partnered with Rutgers to provide math professional development to my teachers. Following that experience I was the Director of Math and Science for a K-12 school district helping children, teachers, and parents look at these content areas in a more meaningful manner. My public education career ended as an interim assistant superintendent in a K-12 district, overseeing curriculum and instruction in all content areas.
More recently, I have been working at the Robert B. Davis Institute for Learning (RBDIL) providing professional development in mathematics to in-service teachers in schools. In addition to using the video mosaic library to enable teachers to watch children engaged in meaningful mathematics, I also provide tasks that actively involve them in rich mathematical explorations. I help teachers make the transition to more thoughtful mathematics in their own classrooms, assisting them in taking an in-depth look at the mathematical reasoning of their students as they engage in more thoughtful mathematics.
You can think of my work with teachers as three cycles consisting of multiple workshops over the course of the school year. Cycle I begins in September when I meet with the teachers to introduce the project and discuss the NCTM process standards. From there we move on to group problem solving. We begin with this problem:
You have two colors of unifix cubes available to build towers. Your task is to make as many different looking towers as possible, each exactly three cubes high. Remember that a tower always points up, with the little knob at the top. Find a way to convince yourself and others that you have found all possible towers three cubes high, and that you have no duplicates.
Before sharing their solutions with the whole group, teachers work in groups of two or three to solve the problem and come up with a convincing argument to justify their solutions.

Following this we watch the PUP Math Stephanie and Dana grade 3 clip where the girls are doing the same task: building 4-tall towers selecting from two colors. This provides an opportunity to discuss patterns, opposites, flips, staircases and elevators.
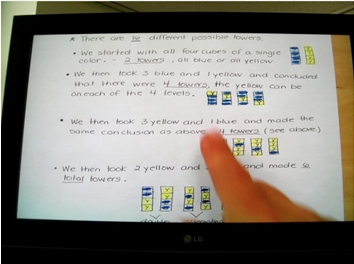
Teachers are asked to make a prediction for towers 3-tall and 5-tall, selecting from 2 colors, and provide their reasoning.
Make a prediction about a solution for finding all possible towers 3 cubes high (without building them). Do you think there will be more, fewer, or the same number of possible towers as you found for towers that were 4 cubes high?
Make a prediction about a solution for finding all possible towers 5 cubes high (without building them). Do you think there will be more, fewer, or the same number of possible towers as you found for towers that were 4 cubes high?
They are tasked with building towers 5-tall, selecting from two colors.
You have two colors of unifix cubes available to build towers. Your task is to make as many different looking towers as possible, each exactly five cubes high. Remember that a tower always points up, with the little knob at the top. Find a way to convince yourself and others that you have found all possible towers five cubes high, and that you have no duplicates.
Once the teachers have an opportunity to share their solutions and provide their convincing arguments, we study the PUP math video of Stephanie and Dana in grade 4, building 5-tall towers, selecting from two colors. We also study the inductive argument used in the Milan/Michelle/Matt/Stephanie video. Before ending our workshop, we discuss the classroom implementation of these problems. Teachers are asked to go back to their own classrooms and use these same tasks with their children, returning with samples of their students' solutions at the next workshop. Additionally, I help teachers in two classes administer the tasks and afterwards spend time with them to discuss the mathematical thinking of their students.
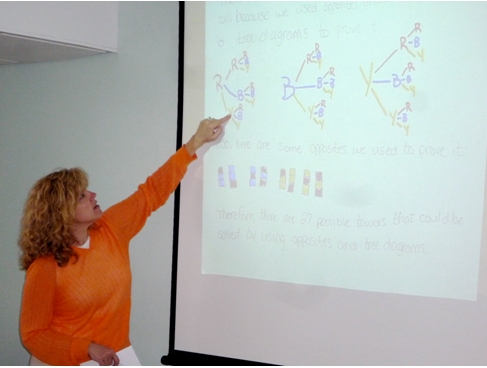
The final workshop in Cycle I provides teachers time to share some of the solutions and convincing arguments of their students. It is fascinating to see children approach the tasks using many of the same strategies and convincing arguments their teachers had used, i.e. proof by cases as shown below:

Finally, we take time at this workshop to study the video of Meredith where she removes the top cube from the towers 4-tall to find towers 3-tall.
Cycle II workshops begin in January. In the first workshop teachers again work in small groups to solve the pizza problem, selecting from four toppings task:
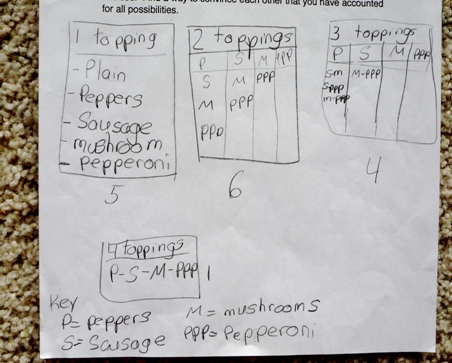
Capri Pizza has asked you to help design a form to keep track of certain pizza choices. They offer a standard "plain" pizza with cheese and tomato sauce. A customer can then select from the following toppings: peppers, sausage, mushrooms, and pepperoni. How many choices for pizza does a customer have? List all possible choices. Find a way to convince each other than you have accounted for all possibilities.
After working on the problem solutions convincing arguments are shared with the whole group. The PUP math video of Brandon's interview with Amy Martino is studied, providing an opportunity to talk about coding, notation, cases, and isomorphism with the towers-4 tall task. As in Cycle I we end the workshop discussing the classroom implementation of this task. Teachers are asked to bring samples of their students' work on this problem to the next workshop. Once again, I assist teachers in two classes administer the task and review the mathematical thinking of their students with them.
The final workshop in Cycle II provides teachers time to share some of the solutions and convincing arguments of their students. It is intriguing to see the children once again approach this task using many of the same notations and convincing arguments their teachers used, i.e. holding constants and proof by cases as shown below:

The Cycle III workshops take place in May. During the first workshop teachers work in small groups to solve the following towers-3 tall problem, selecting from 3 colors.
Find all possible towers that are three cubes tall, selecting from cubes available in three different colors. In the space below, show your solution and provide a convincing argument that you have found them all.
After sharing their solutions and convincing arguments with the entire group, teachers gather in smaller groups to solve Ankur's challenge:
Find all possible towers that are four cubes tall, selecting from cubes available in three different colors so that the resulting towers have at least one of each color. In the space below, show your solution and provide a convincing argument that you have found them all.
Once the teachers have an opportunity to share their solutions and provide their convincing arguments to this extension problem, we study the PUP math video of Romina's Proof.
As we did in each previous cycle we consider the classroom implementation of these tasks, ask for samples of students' work on these problems for the next workshop, and I assist teachers administer the task and discuss the mathematical thinking of their students when the task is completed. This time students (both regular and special education) far surpassed the expectations of their teachers on both the initial task and the extension problem. Teachers were skeptical their students would be able to do Ankur's difficult challenge. But as you see below, 6th graders came up with Romina's proof to Ankur's challenge:

The final workshop in Cycle III allows teachers the opportunity to share some of their students' work. It is amazing to see how the students have grown since the beginning of the school year, now utilizing much more systematic solutions than they did on earlier tasks, as well as providing much more convincing arguments for their work. In addition, the teachers have grown in their ability to recognize what are really good solutions and convincing arguments from their students. We all know the only limits students have are those we place on them. When provided with a chance to show what they can do, students always amaze us with their solutions and surpass our expectations.